Solution to the Informatix puzzle

Informatix is one of the interesting puzzles of the Melbourne University Puzzle Hunt 2013 competition. The plot of the game that year was based on characters from the Asterix & Obelix comics, and each of its puzzles was related to one of the inhabitants of the Gaul village or to one of the Romans. Informatix is ​​one of the villagers. His puzzle was part of the second act of the game. The puzzle was preceded by an image of this character, as well as a brief description of him: "An expert in processing and retrieving data, Informatix always has a tendency to overcomplicate matters."

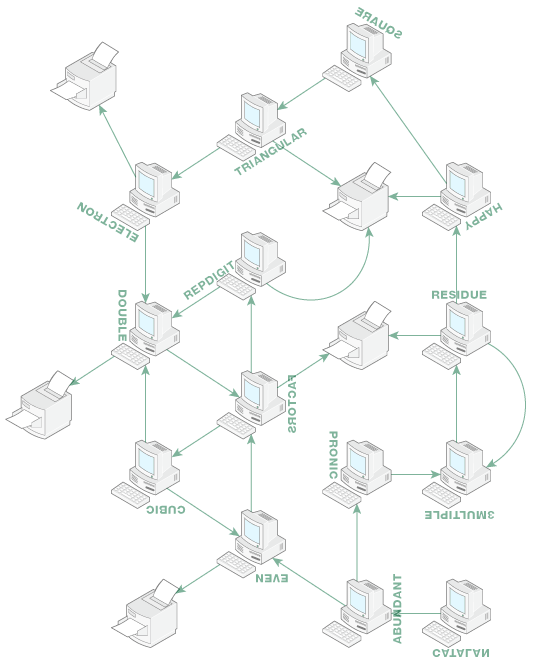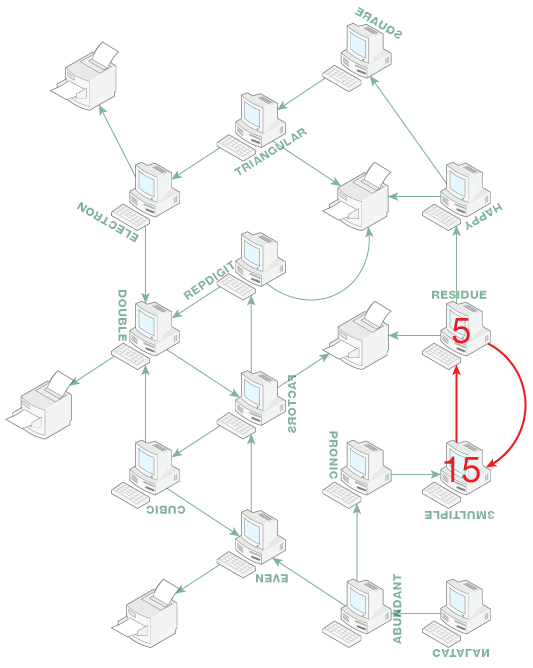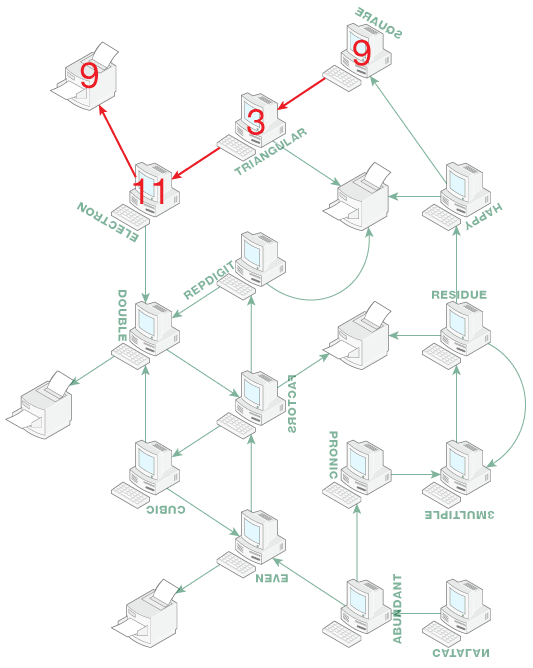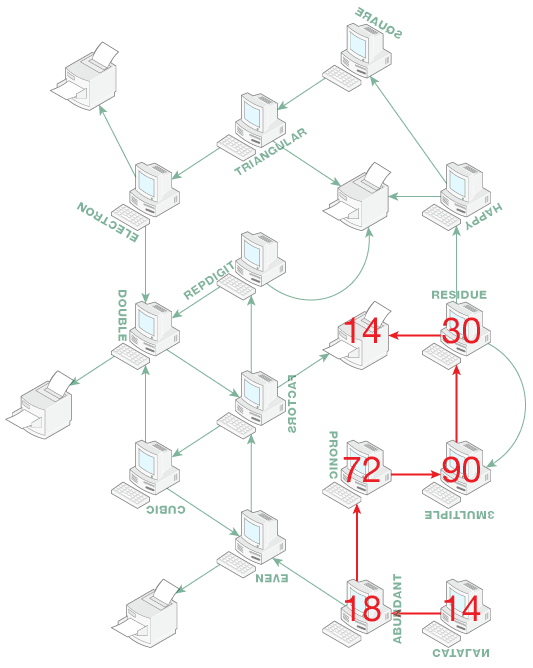
The puzzle itself was a network made up of terminals and printers. The first page of the task contained a graphical representation of this network. The second page of the task contained a table describing transitions between network elements. Each row of this table described one of the 14 terminals. The table had 4 columns. The first column contained the names of the terminals. The second column contained a condition, that should have been checked for the print job's number, when it arrived at the terminal. The third column contained operations on the print job's number, that should have been performed after checking the condition. The fourth column contained the network elements to which the print job had to be sent after processing in the terminal.

In addition, the second page contained a description of the network's functioning when performing a concrete task.

In the computer network pictured, print jobs are routed between terminals in an undeniably complicated fashion as described by the specification table below. Yet, amidst all this obfuscation, the following outcomes were satisfied:
    • of the 14 unique print jobs initiated across the terminals, 12 of them arrived at a printer with
their job number ultimately unchanged;
    • the remaining 2 print jobs arrived back at their original terminal, again with job number
ultimately unchanged.
    • all (non-error returning) routing operations were applied at least once by one or more of the
print jobs
    • at all times, the print job number remained an integer bounded between 1 and 99

The author of this interesting puzzle is Andrew Elvey Price, who in 2013 was Vice-President and then President of the Melbourne University Mathematics and Statistics Society (MUMS).

Obviously, the initial numbers of print jobs are simply a series of numbers from 1 to 14. Therefore, to solve the puzzle it is necessary to assign a unique number from 1 to 14 to each of the 14 terminals, so that the result of the network operation matches the one described in the puzzle.

This voluminous task can be divided into small subtasks: we will assign print jobs to individual terminals one by one in a specific order. Let's start with terminals, that return an error, if the number does not match the condition, since for them there are not so many possible numbers.

For the SQUARE terminal we can only use numbers in the series that are squares: 1, 4 and 9. In this case we will get the following network results.

  • SQUARE(1), TRIANGULAR(1), ELECTRON(9), PRINTER(7), FAIL.
  • SQUARE(4), TRIANGULAR(2), PRINTER(11), FAIL.
  • SQUARE(9), TRIANGULAR(3), ELECTRON(11), PRINTER(9).

We have found the only possible print job number for the SQUARE terminal, this is 9.

For the PRONIC terminal we can only use rectangular numbers. In our series these are 2, 6 and 12.

  • PRONIC(2), 3MULTIPLE(20), #ERROR.
  • PRONIC(6), 3MULTIPLE(24), RESIDUE(8), 3MULTIPLE(18), RESIDUE(6), PRINTER(6).
  • PRONIC(12), 3MULTIPLE(30), RESIDUE(10), HAPPY(3628800), FAIL.

We have found the only possible print job number for the PRONIC terminal, this is 6.

For the 3MULTIPLE terminal we can only use numbers that are multiples of three. Among the numbers in the series, that we have not yet used, these are 3 and 12.

  • 3MULTIPLE(3), RESIDUE(1), HAPPY(1), SQUARE(4), TRIANGULAR(2), PRINTER(11), FAIL.
  • 3MULTIPLE(12), RESIDUE(4), HAPPY(24), PRINTER(12).

We have found the only possible print job number for the 3MULTIPLE terminal , this is 12.

For the CATALAN terminal we can only use Catalan numbers. These in our series are 1, 2, 5 and 14.

  • CATALAN(1), ABUNDANT(5), EVEN(35), PRINTER(10), FAIL.
  • CATALAN(2), ABUNDANT(6), EVEN(42), FACTORS(39), PRINTER(0), FAIL.
  • CATALAN(5), ABUNDANT(9), EVEN(63), PRINTER(2), FAIL.
  • CATALAN(14), ABUNDANT(18), PRONIC(72), 3MULTIPLE(90), RESIDUE(30), PRINTER(14).

We have found the only possible print job number for the CATALAN terminal, this is 14.

Consider next the TRIANGULAR terminal, which checks whether the number n is triangular. If this condition is not met, the terminal will add 9 to n and then send the result to the PRINTER. Obviously, in this case we will not get the original number, which contradicts the conditions of the task. This means, that for this terminal it is enough to consider only the triangular numbers of the series. Of the numbers we have left, these are 1, 3 and 10.

  • TRIANGULAR(1), ELECTRON(9), PRINTER(7), FAIL.
  • TRIANGULAR(3), ELECTRON(11), PRINTER(9), FAIL.
  • TRIANGULAR(10), ELECTRON(18), DOUBLE(7), FACTORS(6), PRINTER(10).

We have found the only possible print job number for the TRIANGULAR terminal, this is 10.

Consider now the HAPPY terminal, which checks whether the number n meets the definition of a happy number. If the condition is not met, the terminal will divide n by 2 and then send the result to the PRINTER. Obviously, in this case we will not get the original number. This means, that for this terminal it is enough to consider only the happy numbers we currently have: 1, 7 and 13.

  • HAPPY(1), SQUARE(4), TRIANGULAR(2), PRINTER(11), FAIL.
  • HAPPY(7), SQUARE(10), #ERROR.
  • HAPPY(13), SQUARE(16), TRIANGULAR(4), PRINTER(13).

We have found the only possible print job number for the HAPPY terminal, this is 13.

Let's move on to the EVEN terminal, which checks whether the number n is even. If this condition is not met, the terminal will find the remainder of dividing n by 9, add 2 to it and then send the result to the PRINTER. Obviously, in this case we will not get the original number. This means, that for this terminal it is enough to consider only the remaining even numbers: 2, 4 and 8. It is easy to establish, that the number 2 is not suitable for this terminal.

  • EVEN(2), FACTORS(-1), FAIL.

Next, it turns out that the sequences for the numbers 4 and 8 will at some point pass through the REPDIGIT terminal, and in this case n will be equal to one: REPDIGIT(1). If we assume, that the condition of REPDIGIT for n = 1 is not satisfied, then the next stage of both sequences will be PRINTER(1), which means that none of the remaining numbers in the series are suitable for the EVEN terminal, which contradicts the conditions of the task. Therefore, the condition of the REPDIGIT terminal for n = 1 is satisfied. This is only possible, if the print job number for the REPDIGIT terminal is 11.

  • REPDIGIT(11), PRINTER(11).

Thus, we have found the print job number for the REPDIGIT terminal, which is 11. Now we can return to the EVEN terminal.

  • EVEN(4), FACTORS(1), REPDIGIT(1), DOUBLE(4), FACTORS(3), CUBIC(4), EVEN(4).
  • EVEN(8), FACTORS(5), CUBIC(6), EVEN(4), …, FAIL.

We have found the only possible print job number for the EVEN terminal, this is 4.

Consider next the ELECTRON terminal, which checks whether the number n corresponds to the number of electrons in one of the atom's electron shells. If this condition is not met, the terminal will subtract 2 from n and then send the result to the PRINTER. Obviously, in this case we will not get the original number. This means, that it's enough to consider only those numbers in the series, that satisfy the terminal condition: 2 and 8.

  • ELECTRON(2), DOUBLE(2), FACTORS(1), REPDIGIT(1), DOUBLE(4), FACTORS(3), CUBIC(4), EVEN(4), …, FAIL.
  • ELECTRON(8), DOUBLE(8), FACTORS(7), CUBIC(8), DOUBLE(16), FACTORS(15), PRINTER(8).

We have found the only possible print job number for the ELECTRON terminal, this is 8.

At the moment we have 5 numbers in the series, that we have not used yet: 1,2,3,5 and 7. Let's try each of them for the ABUNDANT terminal.

  • ABUNDANT(1), EVEN(7), PRINTER(9), FAIL.
  • ABUNDANT(2), EVEN(14), FACTORS(11), CUBIC(12), EVEN(12), FACTORS(9), PRINTER(2).
  • ABUNDANT(3), EVEN(21), PRINTER(5), FAIL.
  • ABUNDANT(5), EVEN(35), PRINTER(10), FAIL.
  • ABUNDANT(7), EVEN(49), PRINTER(6), FAIL.

We have found the only possible print job number for the ABUNDANT terminal, this is 2. 

We have numbers 1,3,5 and 7 left. Let's try each of them for the FACTORS terminal.

  • FACTORS(1), REPDIGIT(1), DOUBLE(4), PRINTER(1).
  • FACTORS(3), CUBIC(4), EVEN(4), …, FAIL.
  • FACTORS(5), CUBIC(6), EVEN(4), …, FAIL.
  • FACTORS(7), CUBIC(8), DOUBLE(16), PRINTER(13), FAIL.

We have found the only possible print job number for the FACTORS terminal, this is 1.

We are left with numbers 3,5 and 7. Let's try each of them for the RESIDUE terminal. 

  • RESIDUE(3), PRINTER(5), FAIL.
  • RESIDUE(5), 3MULTIPLE(15), RESIDUE(5).
  • RESIDUE(7), HAPPY(5040), FAIL.

We have found the only possible print job number for the RESIDUE terminal, this is 5.

We are left with numbers 3 and 7. Let's try each of them for the DOUBLE terminal.

  • DOUBLE(3), FACTORS(2), CUBIC(3), EVEN(1), PRINTER(3).
  • DOUBLE(7), FACTORS(6), PRINTER(10), FAIL.

We have found the only possible print job number for the DOUBLE terminal, this is 3.

Now all that remains is to use the number 7 for the remaining CUBIC terminal.

  • CUBIC(7), EVEN(5), RPINTER(7).

Thus, we solved the problem and obtained the execution sequence for each print job.

  • FACTORS(1), REPDIGIT(1), DOUBLE(4), PRINTER(1).
  • ABUNDANT(2), EVEN(14), FACTORS(11), CUBIC(12), EVEN(12), FACTORS(9), PRINTER(2).
  • DOUBLE(3), FACTORS(2), CUBIC(3), EVEN(1), PRINTER(3).
  • EVEN(4), FACTORS(1), REPDIGIT(1), DOUBLE(4), FACTORS(3), CUBIC(4), EVEN(4).
  • RESIDUE(5), 3MULTIPLE(15), RESIDUE(5).
  • PRONIC(6), 3MULTIPLE(24), RESIDUE(8), 3MULTIPLE(18), RESIDUE(6), PRINTER(6).
  • CUBIC(7), EVEN(5), RPINTER(7).
  • ELECTRON(8), DOUBLE(8), FACTORS(7), CUBIC(8), DOUBLE(16), FACTORS(15), PRINTER(8).
  • SQUARE(9), TRIANGULAR(3), ELECTRON(11), PRINTER(9).
  • TRIANGULAR(10), ELECTRON(18), DOUBLE(7), FACTORS(6), PRINTER(10).
  • REPDIGIT(11), PRINTER(11).
  • 3MULTIPLE(12), RESIDUE(4), HAPPY(24), PRINTER(12).
  • HAPPY(13), SQUARE(16), TRIANGULAR(4), PRINTER(13).
  • CATALAN(14), ABUNDANT(18), PRONIC(72), 3MULTIPLE(90), RESIDUE(30), PRINTER(14).

At this point we have not yet used the graphical representation of the network from the first page of the task. Notably, it allows you to visually track the progress of each print job. It is also interesting that the labels of the terminals are written in a fancy way, using rotations and reflections.

If you graphically depict the progress of each print job, and then rotate and/or flip the diagram, so that the label of its starting terminal can be read correctly, you can see one of the letters of the English alphabet. Together these letters, arranged according to their print job numbers, form a concept from the field of mathematics - LAMBDA CALCULUS. This is the answer to the puzzle.


Comments

Post a Comment

Popular posts from this blog

Cicada 3301 - solution

Image
A few years ago a secret society appeared on the internet. Its activity takes place on the pages of the dark web, the messages of its members are guarded by modern programs for encryption, and it only takes into its ranks those who are able to pass the mysterious game taking place on the  internet. One such game was held in 2012, 2013 and 2014. Each time anyone with internet connection could try their hand. The chain of riddles began from resources such as 4chan , Reddit and Twitter and stretched further gradually taking applicants into the depths of the network. From one riddle to another they had to interpret the mysterious messages of the organizers; look for hidden messages in literary, artistic and musical works; solve ciphers, ancient and modern. Several times the applicants came across telephone numbers, and further instructions were given by a voice on the other end of the line. However the most impressive were the sheets with clues that appeared exactly at the appointed ...
Read more

Cicada 3301 - разгадка

Image
Несколько лет назад во всемирной паутине появилось тайное общество. Его деятельность происходит на страницах темного интернета, на страже сообщений его членов стоят современные программы для шифрования, а в свои ряды оно берет лишь тех, кому под силу пройти таинственную игру, проходящую в сети. По одной такой игре было проведено в 2012, 2013 и 2014 году. Каждый раз попробовать свои силы мог любой желающий, имеющий доступ в интернет. Цепочка загадок начиналась от таких ресурсов как 4chan , Reddit и Twitter и тянулась все дальше, постепенно уводя претендентов в глубины сети. От одной загадки к другой им предстояло истолковывать таинственные сообщения организаторов; искать скрытые послания в литературных, художественных и музыкальных произведениях; разгадывать шифры, древнейшие и современные. Несколько раз претендентам попадались телефонные номера, и дальнейшие указания им давал голос на другом конце провода. Однако наиболее впечатляющими выглядели листы с подсказками, которые точно в н...
Read more

Solution to the Cacophony puzzle

Image
Cacophony  is one of the puzzles of the Melbourne University Puzzle Hunt 2005 competition co-created by the founder of Wikileaks, and likely organizer of the Cicada 3301 community, Julian Assange (the other author of the puzzle is James Saunderson). The puzzle was preceded by a short narrative that moved the script forward. Glad to finally have some lighting, you pull a box of matches out of your pocket and light a candle, grabbing another handful for later. The extra lighting doesn’t help much — the passage is still mostly gray stone, cobwebs and dust. Your wanderings have got your circulation working however, and so you now devote some time to considering how to escape these cellars, and get back to tracking down the coin. The silence of the passages is unexpectedly broken by a distant voice, the same one you heard during yesterday’s mystery, uttering a strange line. “I, Dylan, master mixer of magnificant melodies, shall play you a song.” A brief symphony of dissonance bu...
Read more